Почему сумма всех натуральных чисел равна -1/12
Натуральных чисел бесконечно много, но несмотря на это ученые знают, чему равна их сумма. Но почему она представляет собой такое странное число —-1/12?

Думаете, что если сложить все натуральные числа, то получится бесконечность? Индийский математик еще в начале века показал, что эта сумма будет равна-1/12. Погрузимся в дебри математики и разберемся, что не так с этим значением
Натуральные числа представляют собой целые положительные числа от единицы и до бесконечности. Сумма таких чисел представляет собой классический расходящийся ряд, бесконечная сумма которого должны быть равна бесконечности. Однако существуют способы присвоить сумме этого ряда конечное значение.
Считать сумму расходящихся рядов математики научились еще в XIX веке. Так, например, метод суммирования по Чезаро помог найти сумму знакочередующегося ряда Гранди, который представляет собой последовательность «1-1+1-1+1-...». Эта сумма оказалась равна 1/2. Метод Абеля, разработанный позже, позволяет считать и более сложные ряды, такие как «1-2+3-4+...». Согласно ему, сумма такого ряда будет равна 1/4.
Но ни один из этих методов не позволяет посчитать сумму ряда натуральных чисел. Хорошо, что для этого есть другой метод, который называется регуляризацией дзета-функции Римана. Дзета-функция Римана представляет собой функцию от комплексного переменного s, которая определяется рядом Дирихле. Значение дзета-функции от s равно бесконечной сумме ∑n-s, где суммирование происходит по n от 1 до бесконечности. Если мы возьмем значение дзета-функции от-1, значение членов ряда станет равным натуральным числам: 1-1 = 1, (1/2)-1 = 2, (1/3)-1 = 3... Дзета-функция от-1 в этом случае равна 1 + 2 +3..., то есть сумме натурального ряда.
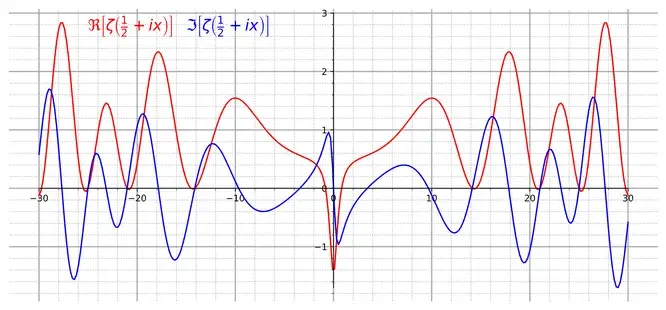
График мнимой и вещественной части дзета-функции можно увидеть на рисунке ниже. Используя соотношение между дзета-функцией Римана и эта-функцией Дирихле можно довольно легко вычислить значение первой. В результате получается, что дзета-функция Римана от-1 равна-1/12. Такое значение получается благодаря тому, что из плоскости вещественных чисел мы переходим в комплексную плоскость.
Если вы дочитали до этого момента, тогда для вас есть приятный бонус — интересный факт. На первый взгляд кажется, что это вычисление суммы ряда натуральных чисел довольно абстрактно и не несет никакой практической пользы. Но на самом деле сумма этого ряда фигурирует в теории струн и даже помогает описать эффект Казимира, заключающийся во взаимном притяжении проводящих незаряженных тел в вакууме под действием квантовых флуктуаций.
интересно?










Проголосуйте, чтобы увидеть результаты

Задача для умных математиков и не только.
Здравствуйте. Благодарю за информирование.
Для меня это слишком мудрено!