Магические квадраты 5 на 5.

Всем привет, меня зовут Андрей, это снова я!

В данной статье я хочу поговорить про магические квадраты.

Магический квадрат - это квадрат размером nxn клеток, в этот квадрат будут вписаны различные цифры (обычно от 1 до n в квадрате, но иногда и из этого правила бывают исключения, то есть начало ведется не с единицы или же разрыв между соседними числами больше единицы).

Разберем несколько вариантов достаточно быстрого получения магического квадрата размером 5 на 5.

Первый вариант:

Возьмем квадрат 5 на 5 и напишем первые 5 цифр следующим образом:

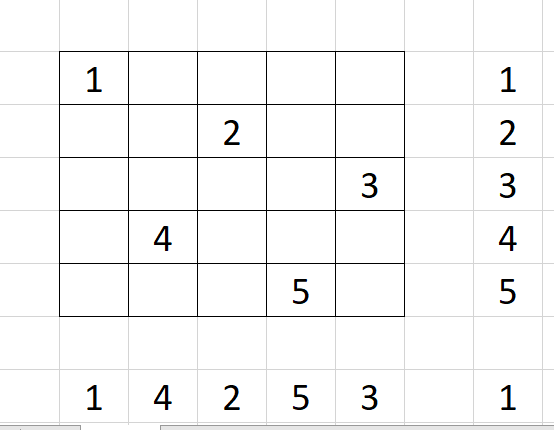
Здесь цифры вне основного квадрата - это суммы по строкам, столбцам, и по основной диагонали. Пока квадрат заполнен не полностью, и поэтому нет ничего удивительного в том, что на данном этапе нет равенства всех нужных сумм.

Затем следующая пятерка - от 6 до 10. Начнем с той клетки, что сразу после цифры 2. Можно, конечно, начать и с других клеток, но нельзя начинать с той клетки, что находится после единицы. А если начать с клетки после пятерки, то не будет нужной суммы на диагоналях. Поэтому пока начнем с той суммы, что после двойки:

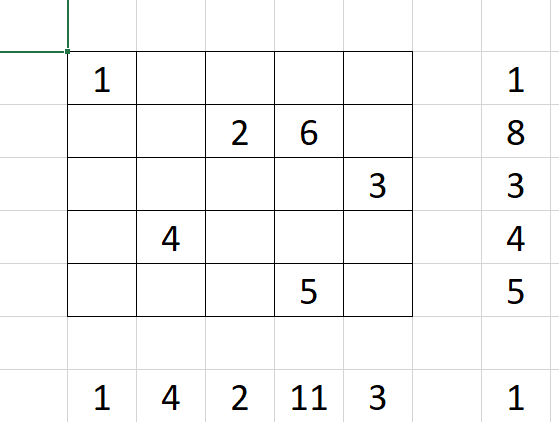
Цифры 7-10 напишем аналогично:

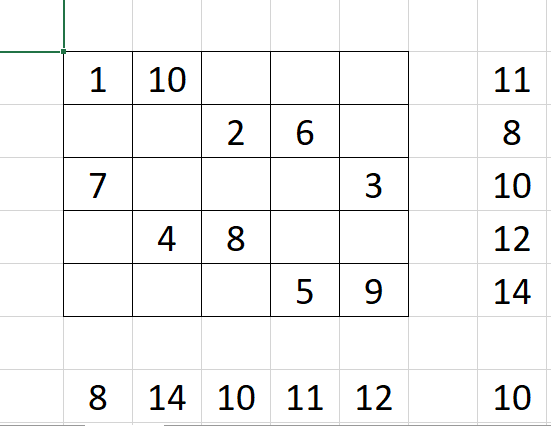
В принципе, остальные пятерки чисел строятся аналогично: 11 будет в той строке, где тройка, 16 - в той строке, где четверка, ну и так далее. И вот что должно получиться:

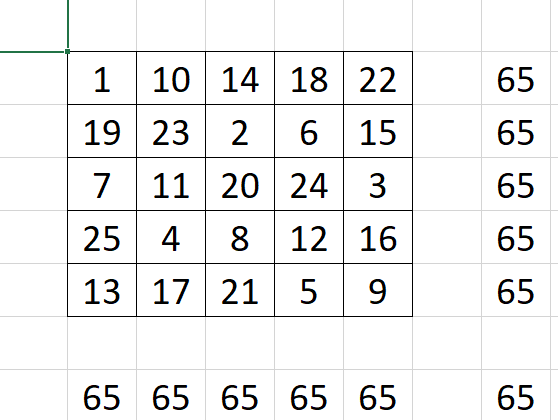
Тут уже с суммами все в порядке. Кстати, при желании можно проверить и сумму второй диагонали, и суммы так называемых "разломанных" диагоналей. Суммы совпадут. Если что, например, 10+19+3+12+21=65 - это была одна из очень многих "разломанных" диагоналей.

Можно сразу же предложить и еще один способ построения магического квадрата размером 5 на 5. Принципы появления цифр-те же, что и в первом случае. Но числа будут меняться не от 1 до 25, а, наоборот, от 25 до 1.

И вот будет результат:

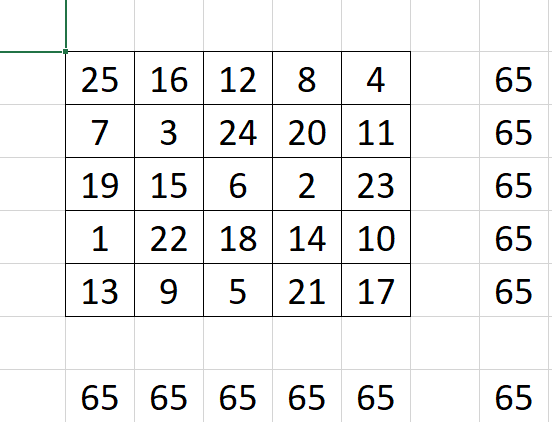
И в этом квадрате тоже, кстати, одна и та же сумма не только у вертикалей, горизонталей и диагоналей, но и у "разломанных" диагоналей. Например, 1+9+12+20+23=65.

Чтобы составить такой квадрат, можно потратить не больше минуты.

И здесь были показаны не все варианты квадратов 5 на 5, а только некоторые варианты. На самом деле всех вариантов намного больше.

А на этом пока всё, всем пока, и до новых встреч!