Они лечат кошек. А убивают подростков
На маркетплейсах свободно можно купить седативные ветеринарные препараты. Наши ...
«Можно короче?»: как эпоха мессенджеров убивает точность и порождает недопонимание
Помните, как в детстве учитель медленно, по слогам, повторял правило, а ты мысленно стонал: «Да понял я, понял!»? А потом, уже взрослым, сам ловишь себя на том, что в десятый раз объясняешь коллеге,...
Telegram остается. В Госдуме пообещали, что мессенджер не будет заблокирован на территории РФ
Зампред председателя комитета Госдумы по информационной политике, технологиям и связи Андрей Свинцов дал ответ на вопрос, который волнует многих российских граждан. Будет ли блокировка Telegram в России?
Почему ваш ребёнок может не идти в школу — даже если за окном не -40
Сейчас зима, и во многих регионах нашей страны морозы крепчают. Приближается ...
Должникам по алиментам запретят брать кредиты и открывать счета в банках. Розыск должников.
В планах наших законодателей стоит главный вопрос об ужесточении мер воздействия на граждан, которые систематически уклоняются от уплаты обязательных платежей на содержание иждивенцев, то есть алиментов.
Telegram до свидания или живи пока? Все переходим на Max? Моё личное мнение про мессенджер Telegram
Я активно пользуюсь этим мессенджером уже достаточно много лет и меня он полностью устраивал и устраивает. Лично я особо не замечала проблем с Telegram, ну разве, что иногда и очень редко.
Ужас или вызов? Почему людям НРАВИТСЯ смотреть на насилие!
недостаточно истребить свидетелей собственной низости. https://hi-news.ru/eto-interesno/lyubite-kriminalnye-shou-i-serialy-uchenye-znayut-pochemu.html В предыдущей публикации"Почему люди платят за жестокость?
Председатель Госдумы Володин сообщил , что могущество страны и ее будущее — в гражданах
Развитие страны зависит от людей, от развития технологий, можно посмотреть ...
Аристон. Статья 72: Цена жизни и ловушка «абсолютной гуманности»
"Весы Ноосферы: Выбор на лезвии бритвы", иллюстрация создана сетью Джемини На краю пропасти Постхристианская мораль провозгласила жизнь каждого человека высшей и равной ценностью. Это звучит благородно,...
Корина подарила Дональду Трампу Нобелевскую премию мира!
Многие говорят, что она за такой подарок хотела получить от Дональда Трампа с благодарность президентство в Венесуэле. Но Дональд Трамп сказал, что Корина хорошая женщина, но в президенты не годится.
У вас сломался холодильник. Как не остаться без денег и холодильника после его ремонта. Схема развода граждан
Во время новогодних каникул со мной произошла неприятная история. На Рождество сломался холодильник, перестал отключаться. Я не настолько богат, чтобы выкидывать старый агрегат и покупать новый.
Статья 2. Великие пророки о будущем России: Феномен «Лидера нового типа»
"Взгляд сквозь инферно", иллюстрация создана сетью Джемини Во второй части ...
Юридическая неделя: от котов до заборов
Пятница — отличный повод оглянуться назад и улыбнуться тому, как разнообразна и неожиданна бывает работа юриста. За одну неделю мне довелось побывать и детективом, и психологом, и даже немного ветеринаром.
00:05
Снегоуборочный мазохизм: депутат рекомендует гражданам не ныть, а взять в руки лопату
В эпоху, когда вертикаль власти достигла поистине гималайских высот, а бюджеты на патриотические фестивали и прочие духовные скрепы лопаются от жира, Госдума выдала очередную жемчужину народной мудрости.



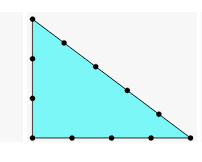






"Пифагоровы штаны на все стороны равны".
НУ да. Вот только к этому треугольнику подходит все, что есть в голосовании.
Правильный ответ- все вышеуказанное.
Ответ - все выше сказанное.
Итак, имеем прямоугольный треугольник с длинами сторон, выраженными целыми числами - Пифагоровы тройки.
Для особо интересующихся обязательно встанет вопрос: "А бывают ли еще подобные тройки?"
Да, бывают.
Самый простой способ - домножить каждое из чисел нашей простой тройки на одно и то же челое число.(Простая это потому, что нельзя нацело разделить каждое из чисел тройки на целое число больше 1).
Домножим на 2, получаем 6,8,10
Домножим на 3, получаем 9,12,15.
Это тоже будут Пифагоровы тройки, но не простые.
А бывают ли еще простые тройки?
Бывают...
Для их получения Евклид явил миру формулу.
Пусть m,n - целые числа, а m>n.....(такое бывает)
Тогда Пифагорова тройка - это три числа
m*m-n*n; 2*m*n; m*m+n*n
Все поразительно просто, как и все в математике.
Например, пусть
m=7, n=4, тогда тройка из этой пары -
33,56,65.
Чтобы узнать, простейшая ли это тройка, нужно разложить каждое из чисел на простые множители.
Если есть один и тот же множитель в каждом из чисел тройки, то эта тройка не является простой.
Если разделить каждое из чисел тройки на их общий множитель, можно получить тройку простую.
Как видите, все просто.
Кстати, наша тройка получилась из Евклидовой пары m=2, n=1.