К вопросу о сумме углов внутри вершин пятиконечных звездочек.

Всем привет, меня зовут Андрей, это снова я!

Сумму углов внутри вершин пятиконечных звездочек удобнее всего считать на примере правильной звездочки.

Добавим кое-что к этой звездочке, чтобы было удобней считать градусные меры углов: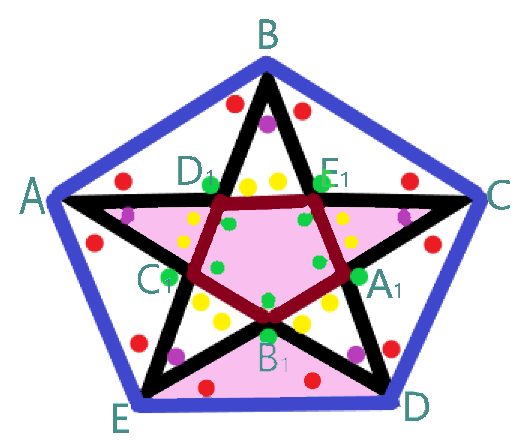

Начнем с того, что на нашем рисунке изображены два пятиугольника. Один из них - маленький пятиугольник - состоит из пяти углов, каждый из которых помечен зеленой точкой.

Поскольку сумма углов каждого пятиугольника равна 540 градусов (при желании это можно доказать, например, сложив суммы углов треугольников EBD, BDC и ABE; сумма углов каждого треугольника известна и равна 180 градусов, значит, сумма углов трех указанных треугольников - это 180*3, то есть 540 (это значит, что каждый из углов правильного пятиугольника равен 108 градусов). Очевидно, что сумма углов этих трех треугольников (540 градусов) и равна сумме "большого" пятиугольника ABCDE).

А теперь можно просто рассмотреть те два треугольника, что я выделил фиолетовым цветом (B1AC и B1ED). Это два равнобедренных треугольника с равными углами при вершинах (в нашем случае речь идет о том, что угол AB1C равен углу EB1D, и эти равные углы отмечены зелеными точками. Как следствие - равенство углов CAD и EDB1.

Поскольку все равные углы на рисунке обозначены точками одного цвета, то можно сказать, что все углы с красной точкой равны всем углам с фиолетовой точкой. А это значит, что пятиконечная звездочка (то есть AD1BE1CA1DB1EC1) в каждой из своей вершин (A, B, C, D, E) разбивает каждый угол большого пятиугольника ABCDE на три равные угла. Поскольку угол при вершине каждого пятиугольника нам уже известен, он равен 108 градусов, то сумма каждого угла при вершине пятиконечной звездочки равна 36 градусов (36=108/3), а сумма всех пяти углов внутри звездочки (на рисунке они выделены фиолетовыми точками) равна 180 градусов (180=5*36).

Итак, сумма углов при вершинах любой пятиконечной звездочки - это 180 градусов. Если это правильная звездочка, то каждый угол будет ровно по 36 градусов.

Кстати, в этой статье я ничего не говорил про те углы, что на рисунке выделены желтыми точками.

Предлагаю гостям моего канала самим вычислить, чему равны эти углы. Пишите в комментариях.

А на этом пока всё, всем пока, и до новых встреч!