Лайфхак о том, как быстро найти площадь треугольника, если известны длины двух сторон и медианы, опущенной на третью сторону.

Всем привет, меня зовут Андрей, это снова я!

В данной статье я хочу рассказать о том, как достаточно быстро можно вычислить площадь треугольника, если известны две стороны этого треугольника, а также медиана этого треугольника, причем и две стороны, и медиана исходят из одной точки.

Приведем пример.

Пусть у нас есть треугольник и одна медиана:

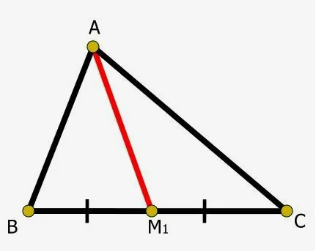
Итак, АМ1 - это медиана, она дели сторону ВС пополам.

Допустим, что известны длины сторон АВ (=7), АМ1 (=6) и АС (=9).

А вот и сам лайфхак: для вычисления площади треугольника АВС можно смело использовать формулу Герона, но предварительно нужно вычислить удвоенную длину медианы. Напомню формулу Герона:

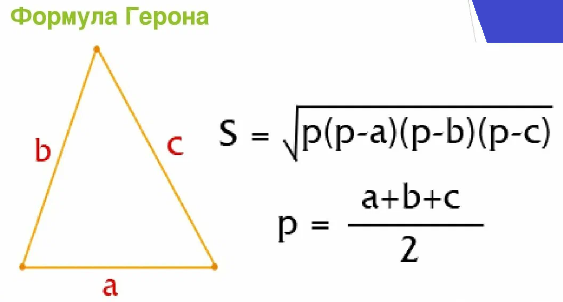
Но у нас пока известны длины только двух сторон. Длину третьей стороны нашего первоначального треугольника мы вычислять не будем; хотя мы и вычислим удвоенную медиану, это еще не значит, что удвоенная медиана будет равна третьей стороне, это утверждение не верное. Но: верно то, что площади этих двух треугольников будут равны.

Конкретно в нашем случае: стороны треугольника 7 и 9, удвоенная медиана будет равна 12. Площадь треугольника со сторонами 7, 12 и 9 будет равна корню из числа 980 (это примерно 31,3 у.е.)

Если интересы доказательства вышесказанного, можно все показать.

Пусть, например, нам известен какой-то треугольник АВС, у него есть медиана ВО. Продлим этот треугольник до параллелограмма. Хотя, в принципе, можно только удвоить медиану и соединить удвоенную медиану с одной из вершин треугольника.

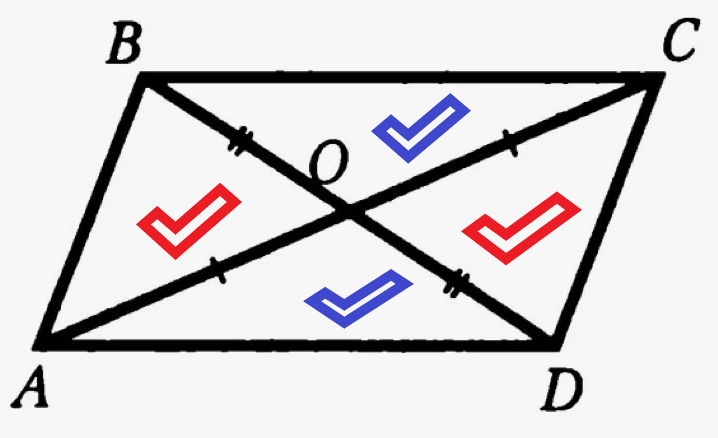
Если мы удвоенную медиану соединим и с точкой А, и с точкой С, то получим параллелограмм ABCD, и в нем уже проведены обе диагонали, причем площади противоположных треугольников будут равны (на рисунке мы отметили треугольники с одинаковой площадью галочками одинакового цвета).

А теперь уточним, что нам даст равенство этих площадей:

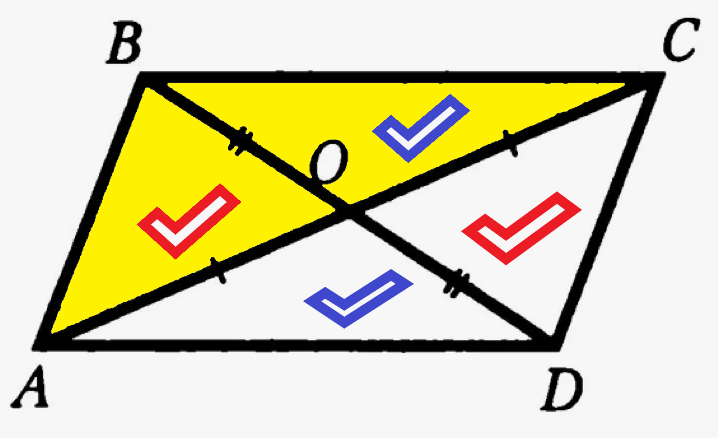
Назовем этот рисунок так: рисунок номер Икс-один. На этом рисунке желтым цветом выделен тот треугольник, который дается в самом начале задаче, у него известны две стороны и медиана.

А теперь второй рисунок:

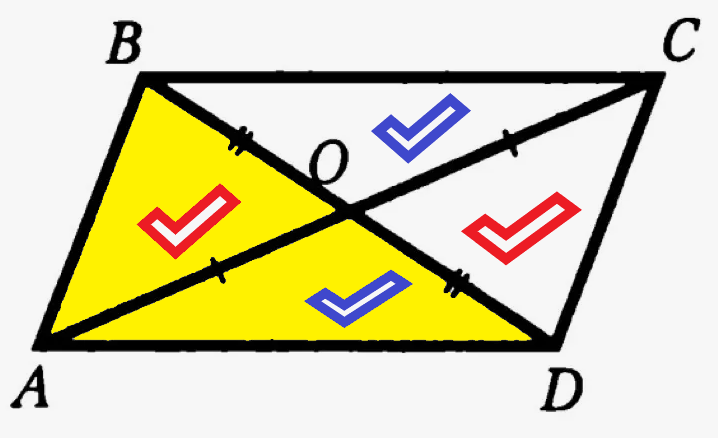
А на втором рисунке (назовем его рисунок икс-два) желтым выделен тот треугольник, у которого известны уже не две, а все три стороны, ведь его третья сторона (AD) - это и есть удвоенная медиана ВО. Кстати, стороны AD и BC равны по построению, это противоположные стороны параллелограмма.

Еще раз скажу, что эта формула применима для любого параллелограмма, хотя не у каждого параллелограмма будут равны диагонали. Если диагонали параллелограмма равны, то это уже будет прямоугольник.

А теперь хотелось бы кое-что пояснить.

Хотя на рисунках икс-один и икс-два площади треугольников, закрашенных желтым цветом, равны, и формула для вычисления их площади одна и та же (мы берем формулу Герона, а для расчета третьей стороны берем удвоенную медиану), и мы видим, что у этих двух треугольников, выделенных желтым цветом, одинаковая площадь, но разные медианы (ведь мы уже говорили, что далеко не всегда у параллелограмма равны диагонали).

Приведем вот какой пример, возьмем ромб, у которого диагонали равны 8 и 6 условных единиц, а стороны равны по 5 у.е. каждая:

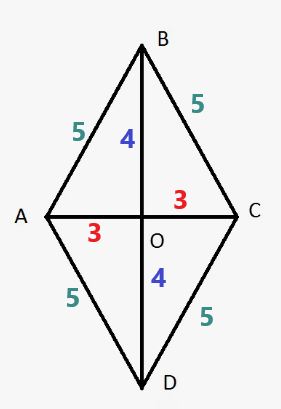
Здесь в треугольнике АВС медиана ВО, и если бы с самого начала было известно только АВ, ВО и ВС, то мы бы для площади треугольника АВС взяли бы стороны АВ (=5), ВС (=5) и ВО (медиана = 4, удвоенная медиана = 8). Площадь треугольника ABD со сторонами 5, 5 и 8 по формуле Герона будет равна 12 у.е.

Можно проверить: полупериметр (p) = (5+5+8)/2 = 9

p-a=9-5=4

p-b=9-5=4

p-c=9-8=1

S=корень(9*4*4*1)=12.

Но если ту же площадь вычислить через треугольник ABС, у него будут стороны 5, 5 и 6, и площадь этого треугольника тоже будет равна 12 у.е. - хоть по формуле Герона, хоть по другой формуле. Но мы пока ведем речь о формуле Герона:

p=(5+5+6)/2 = 8

p-a=8-5=3

p-b=8-5=3

p-c=8-6=2

S=корень(8*3*3*2)=12

Хоть мы и брали каждый раз одинаковые стороны, но разные медианы, результат получился одинаковый.

Итак, повторю: если известны длины двух сторон треугольника и медиана на третью сторону, то для площади этого треугольника можно пользоваться формулой Герона, предварительно вычислив удвоенную длину медианы.

А на этом пока всё, всем пока, и до новых встреч!