Радиус описанной и вписанной окружности: Формулы и примеры
Здравствуйте мои дорогие подписчики и гости сайта 9111.ru!
На самом деле эту тему проходят еще в начальных классах обычной школы. И все, кто хорошо учился, сразу смогут сказать, о чем идет речь. Ну, или хотя бы точно понять, что РАДИУС как-то связан с окружностью.
Что такое радиус
И действительно:
Радиус – это отрезок, который начинается в центре окружности и заканчивается в любой точке ее поверхности. В то же время так называется и длина этого отрезка.
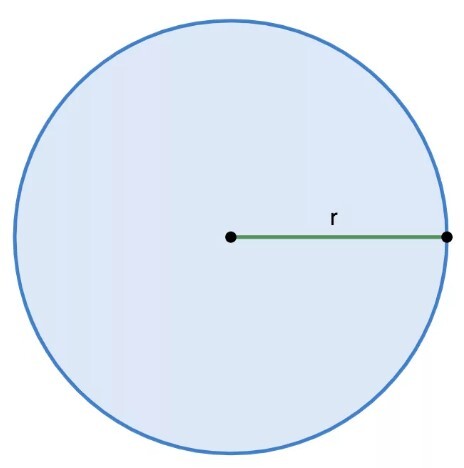
Вот так это выглядит графически.
**************************************
Само слово РАДИУС имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или «спица колеса». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.
Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.
Кстати, есть еще несколько значений слова РАДИУС:
- Размер охвата чего-нибудь или сфера распространения. Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
- В анатомии этим словом обозначают Лучевую кость предплечья.
Но, конечно, нас интересует РАДИУС как математический термин. А потому и продолжим говорить именно о нем.
Радиус и диаметр
Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.
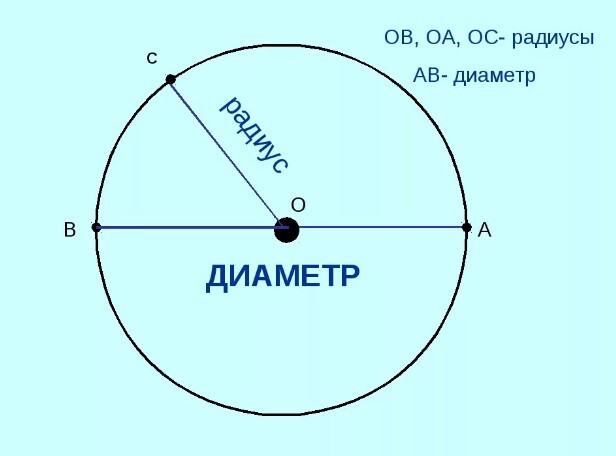
Обозначается диаметр также первой буквой своего слова – D или d.
Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.
А именно:
Длина диаметра равна удвоенной длине радиуса.

Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2.
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

Формулы для радиуса описанной окружности
Найти радиус описанной окружности треугольника по сторонам
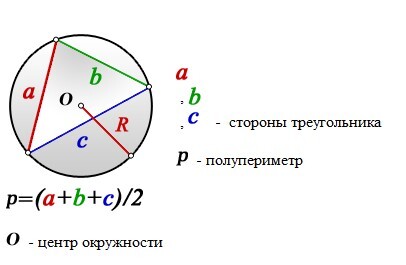
Формула радиуса описанной окружности треугольника (R ) :
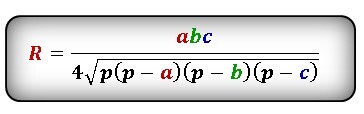
Найти радиус описанной окружности равностороннего треугольника по стороне или высоте
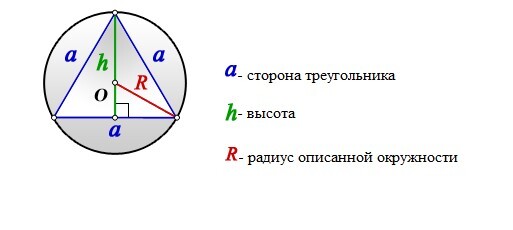
Формула радиуса описанной окружности равностороннего треугольника через его сторону:

Формула радиуса описанной окружности равностороннего треугольника через высоту:
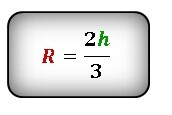
Найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
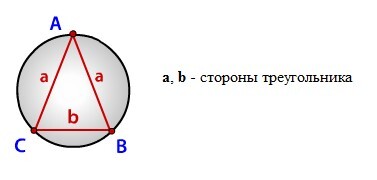
Формула радиуса описанной окружности равнобедренного треугольника (R):

Найти радиус описанной окружности прямоугольного треугольника по катетам
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.

Формула радиуса описанной окружности прямоугольного треугольника (R):
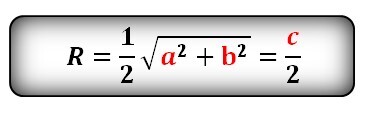
Радиус описанной окружности трапеции по сторонам и диагонали

Формула радиуса описанной окружности равнобокой трапеции, (R)
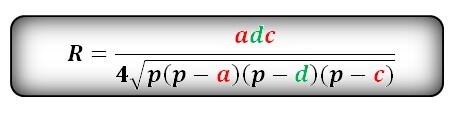
Найти радиус описанной окружности около квадрата
Радиус описанной окружности квадрата равен половине его диагонали
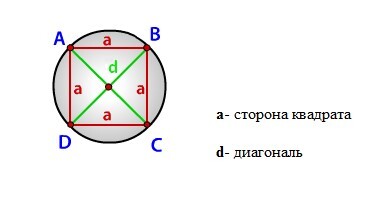
Формула радиуса описанной окружности квадрата (R):

Радиус описанной окружности прямоугольника по сторонам
Радиус описанной окружности прямоугольника равен половине его диагонали
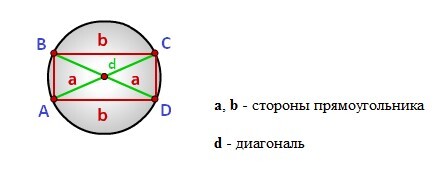
Формула радиуса описанной окружности прямоугольника (R):
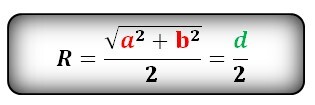
Радиус описанной окружности правильного многоугольника
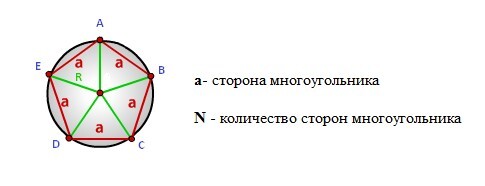
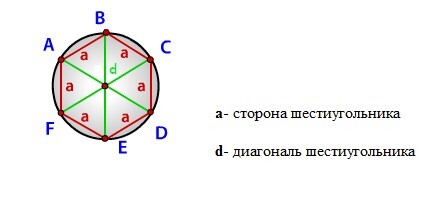
Формула радиуса описанной окружности правильного многоугольника, (R):
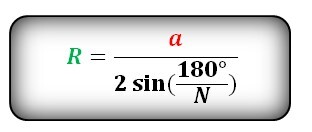
Радиус описанной окружности правильного шестиугольника
Радиус описанной окружности правильного шестиугольника (R):

Формулы для радиуса вписанной окружности
Радиус вписанной окружности в треугольник

Формула радиуса вписанной окружности в треугольник (r):

Радиус вписанной окружности в равносторонний треугольник
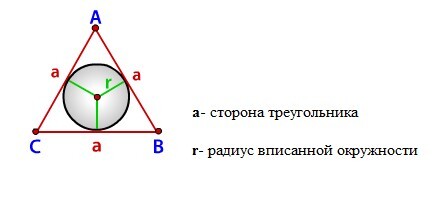
Формула для радиуса вписанной окружности в равносторонний треугольник (r):

Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны (r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол (r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту (r ) :

Радиус вписанной окружности в прямоугольный треугольник

Формула радиуса вписанной окружности в прямоугольный треугольник (r):
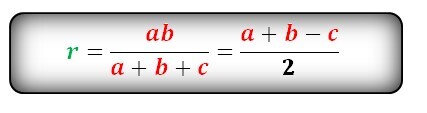
Радиус вписанной окружности в равнобочную трапецию
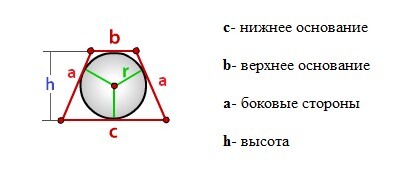
Формула радиуса вписанной окружности равнобочной трапеции (r):
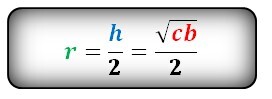
Радиус вписанной окружности в квадрат
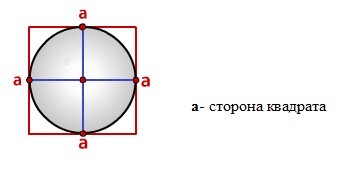
Формула радиуса вписанной окружности в квадрат (r):

Радиус вписанной окружности в ромб
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

Формула радиуса вписанной окружности в ромб через диагонали (r ) :

Формула радиуса вписанной окружности в ромб через сторону и угол (r ) :
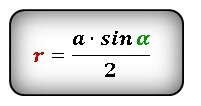
Формула радиуса вписанной окружности в ромб через диагональ и угол (r ) :

Формула радиуса вписанной окружности в ромб через диагональ и сторону (r ) :

2. Радиус вписанной окружности ромба, равен половине его высоты

Формула радиуса вписанной окружности в ромб (r ) :

Радиус вписанной окружности в правильный многоугольник

Формула радиуса вписанной окружности в правильный многоугольник, (r):

Радиус вписанной окружности в шестиугольник
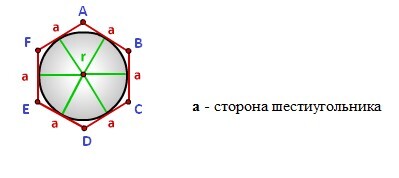
Формула радиуса вписанной окружности в шестиугольник, (r):

Примеры задач
Задание 1
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.
Решение
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:

Остается только применить соответствующую формулу для вычисления радиуса круга:

Задание 2
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.
Решение
Воспользуемся подходящей формулой, подставив в нее известные значения:

Всем спасибо и приятного просмотра! Если понравилась публикация подписывайтесь и ставьте палец вверх!
Источники:
- https://KtoNaNovenkogo.ru/voprosy-i-otvety/radius-chto-ehto-takoe-kak-najti-radius-okruzhnosti-formula.html
- https://MicroExcel.ru/radius-kruga/
- https://www-formula.ru/2011-09-24-00-42-22
- https://www-formula.ru/2011-09-24-00-40-48
- https://MicroExcel.ru/radius-vpisannogo-v-treugolnik-kruga/





Проголосуйте, чтобы увидеть результаты



Приятно было освежить знания.
Давно не пользовался ими в этой сфере.
Спасибо, Дмитрий!
затхлость проходит?
А ещё способы освежения?
Нравится?
Афигеть! Геометрия стала дистанционной?
Сразу вспомнила школу).