Гипотеза Коллатца и один пример расчета по этой методике

Если сказать вкратце, гипотеза Коллатца - это одна из нерешенных задач (или проблем) в математике. Сама гипотезе есть, проверена была на нескольких миллионах чисел, но конкретного доказательства до сих пор не существует.

Эта гипотеза состоит в следующем. Берем любое число. Если оно четное, то делим пополам. А если не четное, то умножаем на 3 и сразу после этого прибавляем единицу (если само число х, то в результате преобразований получаем 3 х+1). И так проделываем несколько раз. Суть этой гипотезы заключается в том, что какое бы мы ни взяли число, рано или поздно мы получим единицу.

Конечно же, если мы какое-о нечетное число умножим на 3, то это будет нечетное число, а после прибавления к нечетному числу единицы мы обязательно получим четное число.

Другими словами, мы, беря любое нечетное число, можем произвести два шага сразу (сначала умножить на 3 и прибавить единицу, а затем полученный результат разделить пополам).

Действительно, 0,5* (3 х+1) = 1,5 х+0,5 = (15 х+5)/10

Приведем несколько примеров.

Пусть у нас есть число 97865891.

Почему именно это число? Однажды в одном из финалов шоу "Удивительные люди" человек вычислял в уме корень 9999-й степени из очень длинного числа, в котором было почти 80 тысяч цифр. Это подкоренное число и было 97865891.

Так вот, применяя операции по гипотезе Коллатца (ну или по методике, по алгоритму Коллатца) всего лишь 143 раза, мы, действительно, получим единицу.

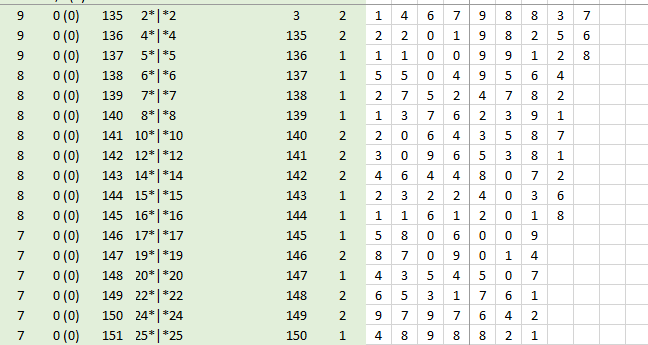
Итак, уже после шага 25 мы имеем число 4898821 (остальные числа и цифры имеют скорее служебную, техническую, вспомогательную направленность; например, самый левый столбец - это количество цифр в основном числе; основные числа, разбитые на отдельные цифры, идут на белом фоне).

Продолжим:

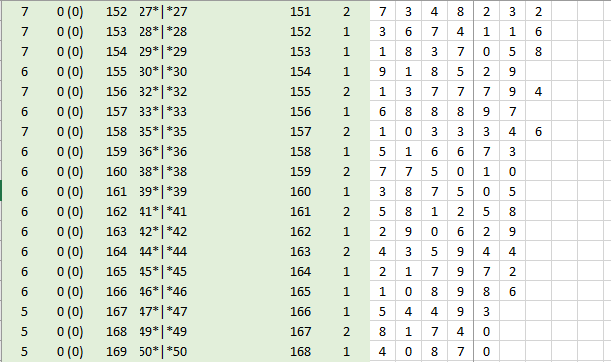
После шага 50 у нас уже появляется число 40870. Это намного меньше первоначального числа.

Продолжим расчеты.

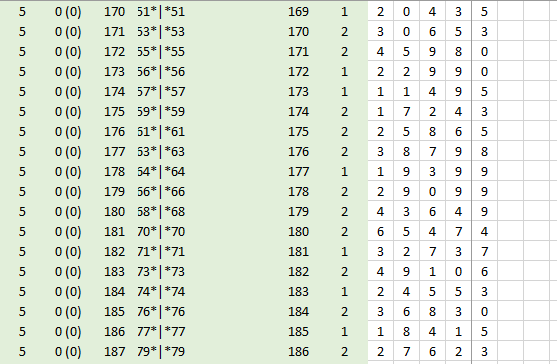
Да, часто бывает так, что расчеты словно топчутся на одном месте. Это бывает в тех случаях, когда велик процент нечетных чисел среди всех промежуточных результатов, особенно если речь идет о небольшом интервале, что и наблюдается в данном случае. С четными числа намного проще - там просто надо их делить пополам, поэтому когда встречаются много четных чисел подряд, то идет и быстрое уменьшение длины цифр, и уменьшение минимального числа из всего списка.

Продолжим расчеты.

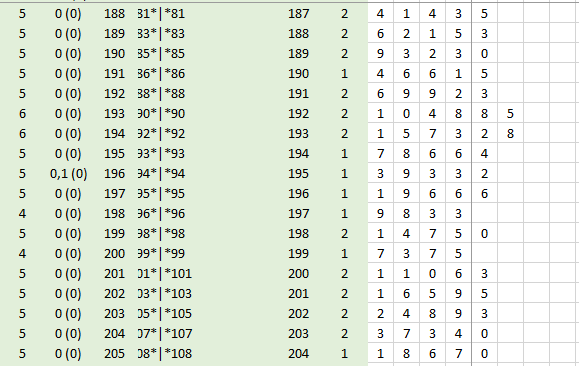
Выполнено 108 шагов, получено число 18670. Пусть медленно, но итоговое число все же уменьшается.

Идем дальше.

После шага 132 у нас получилось число 52. Финиш близок.

Итак, всего было 143 шага, и получен нужный результат - то есть единица.

Если кому интересна эта тема, я с удовольствием в будущем напишу про разложение других чисел по методике Коллатца, ну или хотя бы приведу конечные результаты, например, количество шагов, после которых мы реально получим единицу.

А на этом пока всё, всем пока, и до новых встреч!