Суд встанет на вашу сторону — даже если вы не вышли из дома
Сейчас зима, и погодные циклоны порой сильно усложняют нам жизнь. А можно ли при непогоде ...
🌳 За незаконную вырубку леса задержан директор нацпарка «Куршская коса», который входит в список объектов Всемирного наследия ЮНЕСКО
Уголовное дело возбудили против Анатолия Калины, который 15 лет руководил территорией национального парка «Куршская коса». Это место является природным сокровищем России и объектом Всемирного наследия ЮНЕСКО.
00:58
«Заработала или подарили?»: почему красивая женщина сразу получает клеймо содержанки?
Сегодня хочу поговорить о наболевшем. Заметили, как у нас в обществе (и особенно ...
Назван окончательный срок блокировки WhatsApp в России
Стала известна информация, что в 2026 Роскомнадзор может окончательно заблокировать в РФ. Не знаю, как у Вас, но у меня WhatsApp перестал работать еще до Нового года. Не отправляется ни-че-го,...
Пока русские дети массово умирают в роддомах: Россия спонсирует роддома Таджикистана
Всю страну повергла в шок новость о массовых смертях наших маленьких новорожденных в Новокузнецке, где за новогодние праздники умерли 11 новорожденных малышей. По предварительной версии следствия,...
Юрист в МФЦ: теперь бесплатно! Идея Делягина, которая сэкономит вам деньги и нервы
Знаете, как бывает: пришёл в МФЦ за справкой, а заодно хочется спросить — а как правильно ...
Мир на Украине зависит от США и России или от Зеленского?
С кем бы я ни вел беседы об урегулировании конфликта на Украине, почти все считают, что это зависит от России и США. Поэтому возобновление переговорного процесса между этими странами очень важно.
Военные европейских стран НАТО начали прибывать в Гренландию
Дональд Трамп предъявляет претензии и свои права на остров, объясняя это стратегической важностью Гренландии для США. Для того, чтобы защитить жителей и предотвратить военное столкновение союзников по альянсу,
Появятся ли британцы на Украине?
Уже не один раз российские новостные агентства показывали по телевизору и рассказывали
Кредитные истории: можно ли им верить на 100%, отчет в трех кредитных бюро в один день - а результаты такие разные
Наступил новый 2026 год, праздники закончились и снова все вернулись к обычной жизни. Раньше эта услуга была только на платной основе. Банки, и не только, дополнительно зарабатывали на этом деньги,...
Роберт Бартини. Статья 40: Кристаллизация воли – Заговор Равных
"Маскировка чести: Заговор равных", иллюстрация создана сетью Джемини В этой ...
Американцы подали в суд на РФ, Минфин, ЦБ и ФНБ с требованием расплатиться по долгам царской России в размере $225 млрд
Американский Инвестиционный фонд подал в суд иск к России, Минфину, Центральному ...



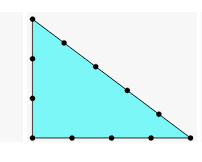






"Пифагоровы штаны на все стороны равны".
НУ да. Вот только к этому треугольнику подходит все, что есть в голосовании.
Правильный ответ- все вышеуказанное.
Ответ - все выше сказанное.
Итак, имеем прямоугольный треугольник с длинами сторон, выраженными целыми числами - Пифагоровы тройки.
Для особо интересующихся обязательно встанет вопрос: "А бывают ли еще подобные тройки?"
Да, бывают.
Самый простой способ - домножить каждое из чисел нашей простой тройки на одно и то же челое число.(Простая это потому, что нельзя нацело разделить каждое из чисел тройки на целое число больше 1).
Домножим на 2, получаем 6,8,10
Домножим на 3, получаем 9,12,15.
Это тоже будут Пифагоровы тройки, но не простые.
А бывают ли еще простые тройки?
Бывают...
Для их получения Евклид явил миру формулу.
Пусть m,n - целые числа, а m>n.....(такое бывает)
Тогда Пифагорова тройка - это три числа
m*m-n*n; 2*m*n; m*m+n*n
Все поразительно просто, как и все в математике.
Например, пусть
m=7, n=4, тогда тройка из этой пары -
33,56,65.
Чтобы узнать, простейшая ли это тройка, нужно разложить каждое из чисел на простые множители.
Если есть один и тот же множитель в каждом из чисел тройки, то эта тройка не является простой.
Если разделить каждое из чисел тройки на их общий множитель, можно получить тройку простую.
Как видите, все просто.
Кстати, наша тройка получилась из Евклидовой пары m=2, n=1.